An introduction to Chaos Theory

"Deviner avant de démontrer! Ai-je besoin de rappeler que c’est ainsi que se sont faites toutes les découverte importantes. Guessing before proving! Need I remind you that it is so that all important discoveries have been made?
The scientist does not study nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful. If nature were not beautiful, it would not be worth knowing, and if nature were not worth knowing, life would not be worth living”. Jules Henri Poincaré
1. Introduction to Chaos
Ok, I agree, this quote seems a bit pretentious but it captures my feelings about chaos theory which is one of the most exciting topics I’ve come across in my career! In this paper we investigate chaos theory which will support my first blog on the role of PSpice simulation. Chaos theory, a subset of ‘complex- ity theory’. The science of complexity involves the principle of Self-Organizing Criticality,of which the human brain is a great example, where large neurons organize themselves to form an extremely complex connective network which can solve complex problems with a rapidity still not matched by present day computers. It has been postulated by Walter Freeman III how chaos plays an important role in brain functioning and attempts to explain how it operates as fast as it does! This short introduction to chaos theory will outline how we can use a chaotic source to produce unlimited amounts of ‘cryptographic keys’ for secure saving of data in Cloud computing (CC). The word chaos is from the Greek verb to gape open and normally used to mean total disarray such as seen in the aftermath of an explosion. However, we will see that chaos the- ory is anything but total disarray! A little history to outline how chaos theory developed by a relatively few people: The Greek philosopher, Anaxagoras [1], the great Scottish scientist, James Clerk Maxwell (1876), Hadamard (1898) [2], Poincaré in 1890 [3], [4] and Andronov (1929) [5]. The exploration of chaos (it wasn’t called chaos theory yet) continued in a haphazard fashion and in 1975, Tien-Yien Li and James A. Yorke, introduced the term ‘Chaos’ in their paper ”Period Three Implies Chaos” [6].
Chaos theory is the science of nonlinear topics and has many potential applications in engineering, physics, medicine, biology, and economics, etc. Engineers have focused on the linear aspects of engineering and largely ignored the interesting nonlinear world. Indeed, the world of mathematics and science has, until recently, ignored nonlinear system which are “unsolvable” in the traditional sense. However, to get over this we can make nonlinear systems approximately linear for small perturbations about points of equilibrium called fixed points (FP). We will use FPs to design a suitable threshold point using chaos source signals later. Of course, nonlinear design techniques were used when designing signal generators, class C power amplifiers, modulators, etc., but this was in a limited sense only and didn’t consider any chaotic aspects.
Nature, by and large, is not linear and straight lines are rarely, if ever, ob- served in the natural World. In essence, electrical engineers have dismissed nature’s evolutionary design techniques and mainly considered linear designs. Nature, through evolutionary steps, created some of the most complex structures in the known universe, of which the human brain is its finest example. Nonlinearity is a necessary condition for equations to be chaotic, such equations which cannot really be solved analytically and requires the power of personal computers to provide a solution.
King Oscar II of Sweden and Norway (1872-1907), announced a competition for a prize of 2500 kroner to celebrate his 60th birthday to anyone who could prove that the Solar system was stable and would not fly apart at some future date. Jules Henri Poincaré (1854-1912), who was a brilliant mathematician and physicist [´e], took on the challenge and won the prize for his paper ‘sur le problème `a trois corps’ ‘On the problem of three bodies and the equations of equilibrium”. Nonlinear system dynamics was first investigated by this brilliant French polymath who recognized chaos as an almost impossible topic to analyze mathematically.
Another French mathematician, Edvard Phragmen, pointed out serious mistakes in Poincaré's orbital stability calculations and resulted in Poincaré with- drawing his book from circulation. Nevertheless, Poincaré flawed solution created new areas of maths such as topology and the study of dynamical systems. He is considered by many to be the ‘Father of Chaos Theory’. On a historical note, the three-body problem was eventually solved by the Finnish Mathematician, Karl Sundman in 1912, but the solution converged so slowly that it wasn’t useful!
Poincaré also invented a new ways of thinking using pictures to visualize problems rather than rigorous mathematical analysis. He added to the concept of phase space by visualizing the trajectory of a complex dynamical system as it evolves. His work on two-dimensional transverse slices from complex three- dimensional flows is called a Poincaré section and will be examined later. This revolutionized continuous, hard-to-visualize 3-D systems into much simpler 2-D digital maps. Henri Poincaré also introduced the important concept called bifurcation in a mathematics paper in 1885 [7]. However, chaos theory was not investigated for a long time after Poincaré except for a few mathematicians such as George David Birkhoff (1884-1944) and some European and Russian mathematicians.
In the mid-sixties Edward Lorenz, a meteorologist/mathematician (a student of Birkhoff), discovered quite by accident, one of the hallmarks of chaos theory whilst modeling weather patterns,- Sensitivity to Initial Conditions (SIC) [8]. Weather patterns, dripping taps, etc. are examples of nonlinear dynamical systems which exhibit chaotic behavior and are highly sensitive to initial conditions (IC). The trajectory, starting from some IC, of these chaotic systems will proceed along a certain path, however, setting the IC to a tiny, but different starting value, will produce a very different trajectory/path. Thus, systems that are sensitivity to initial conditions, means that the final output will be vastly different for very small changes in the initial conditions. This is often referred to as the “Butterfly effect”, a term mentioned in a lecture by Edward Lorenz in 1972 -“Predictability: Does the flap of a butterfly’s wings in Brazil set off a Tornado in Texas”[9].
Chaotic systems are deterministic over a short period, hence we can make pre- dictions in weather patterns up to about ten about days. According to Strogatz’s chaos videos “Does the butterfly effect imply that chaotic systems are unpredictable? –No, they are predictable in the short term because of their deterministic character, but they become unpredictable after a certain amount of time, called the horizon of predictability [10] and is the time required for tiny errors to double in size. The Solar system trajectory is accurate to about 5 million years.” After that, the path will deviate significantly. Another person who has been ignored in chaos literature, but who contributed to chaos theory, is Mary Lucy Cartwright [1900-1998] [11].
1.1Nonlinear Dynamical Chaotic Systems
Chaotic systems are classified as conservative or dissipative. Astronomical systems are examples of conservative systems and sometimes referred to as ‘Physi- cist’s chaos’, where the phase space volume remains unchanged but changes its overall shape in time. Dissipative systems, or ‘Engineer’s chaos’, are considered in this blog and have a phase space volume that shrinks with time and contain ‘Strange Attractors’. Dissipative systems are further classified further as continuous and discrete; continuous system-analogue systems operate over all time, whereas discrete or digital systems, exist at discrete periods of time.
Another classification for nonlinear chaotic oscillatory systems, autonomous and non-autonomous. Systems that have an external exciting input signal are called non-autonomous, meaning time is involved. The equations on the left-hand side of these system normally show a periodic forcing input signal. When no external input is applied to the chaotic system and which do not contain time-dependent parameters, they are said to be autonomous. An example of an autonomous system is the Lorenz equation system examined in the first blog and which models atmospheric convection. On the other hand, a non-autonomous chaotic example is the chaotic Duffing nonlinear oscillator which has an external cosine forcing input signal, cosωt.
1.2 Chaos applications
There are many potential applications for chaos but in this blog we look at a cryptographic application for securing data in the Cloud. A dynamic chaotic system equation contains state variables and constants to represent the ‘state’ of the system in phase space with time. The trajectory (a flow or orbit), traces the history of the system as time evolves. For example, this could be the speed of a planet in space or a particle in space, with measurable states such as velocity, acceleration. However, the dynamical systems in this treatment are concerned with state changes of voltage and current in electronic circuits starting from some initial condition and produce chaotic signals.
1.3 Phase Space
Phase Space is a mathematical representation of the state of a system in two or three dimensions and there is much confusion over who introduced the concept of phase space. A fine paper by David Nolte explains the history of this concept for those of you interested. The concept of phase space was mistakenly attributed to Liouville and Gibbs (1902) but it was Boltzmann who introduced the concept. He gave credit to Liouville thus doing himself out of the honor of being its creator. Henri Poincaré and the Irish mathematician, Sir William Edwin Hamilton (1806-65), along with Carl Jacobi, also contributed to this concept. In a 1971 paper, ‘On the Nature of Turbulence’ by David Ruelle and Floris Takens, they described how variables in phase space trace out two and three-dimensional shapes which they called ‘strange attractors. The number of variables describing the attractor is its dimensionality.
Figure 1 shows a 3-D picture of Lorenz phase space with a Poincaré section through the phase space.
In discrete-time systems, the flow is called a map or orbit and produce time-voltage or time-current, vectors. Jules Henri Poincaré explained the impossibility of getting meaningful results from these time series and introduced the Poincaré section - a beautifully-simple mathematical technique for reducing the dimensionality of the 3-D phase/state space by one and thus simplified its complexity. We need at least three state variables for an autonomous continuous chaotic system - a requirement for the Poincar´e-Bendixson theorem. For a 2-D sampled system, the third dimension comes from sampled time. Differential equations solve the trajectory of continuous systems and difference equations solve the trajectory of discrete chaotic maps.
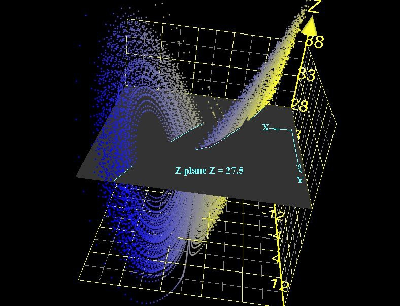
Figure 1: Lorenz 3D phase space showing a Poincaré section
A question that could be asked “What is the difference between a random (noisy or stochastic) signal and a chaotic deterministic signal”? To answer this question let’s consider the simple schematic in Figure 3 which shows two generators; one is a PSpice noise generator introduced in the present version, and the other is chaotic signal from a Lorenz generator, both are attached to an analog delay achieved using a correctly terminated and buffered T part. The delay is necessary to try and correlate past and present values. For a noise signal there should be no correlation between past and present values. A chaotic time series is a stochastic signal that occurring in a deterministic way, whereas a random noisy signal is completely stochastic. Individual trajectories in a chaotic time series are totally unpredictable, but the overall behaviour is not.
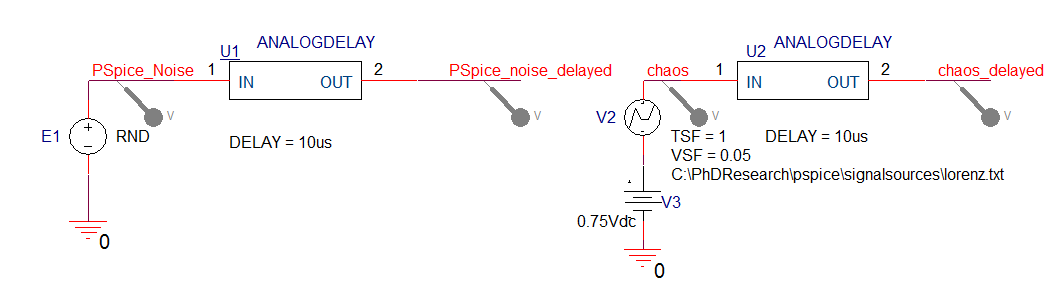
Figure 2: Noise and chaos signals
The outputs from these generators produce two-time series that look similar. However, if we delay each signal by a suitable amount, and plot the delayed versus the undelayed signal, we get results shown in Figure 3.
We see for the random noise signal, there is no correlation between the delayed and undelayed signals and the attractor shows this very well.
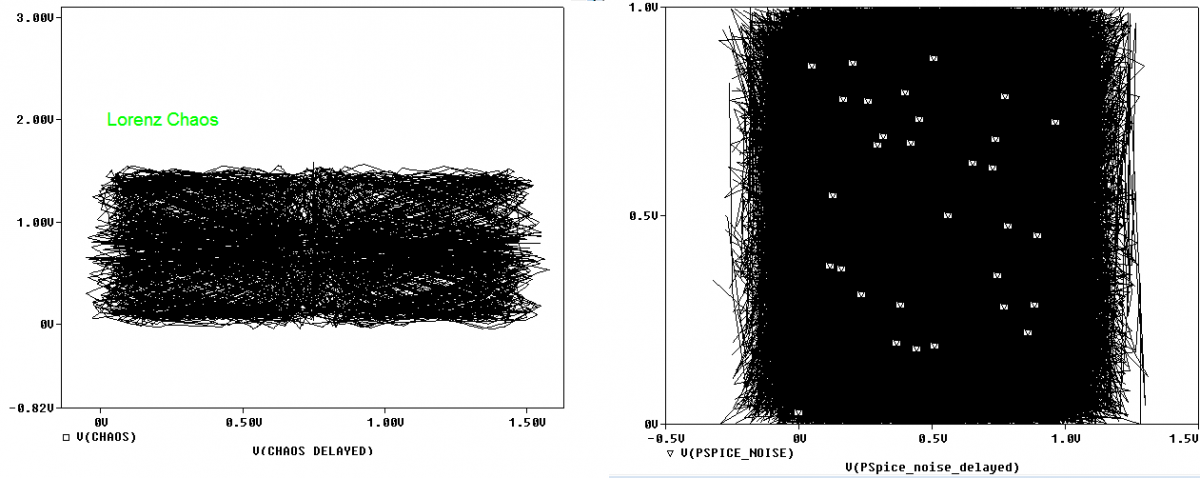
Figure 3. Chaotic and noise attractors showing no correlation between the signal and a delayed version of it.
References
[1] Anaxagoras (456 B.C.E.). On the mind. Fragment No. 12, English translation in R¨ossler, pp. 11-12.
[2] Hadamard J.S. (1989). Les surfaces `a coubures oppos´ees et leurs lignes g´eodesique. Journal de Math´ematique Pure et Appliqu´ee, 4, 27-73.
[3] Poincar´e, H. (1890). Sur les ´equations de la dynamique et le probl`eme de trios corps. Acta Mathematica, 13, 1-270.
[4] Poincar´e, H. (1908). Science et m´ethode. Paris: Ernest Flammarion. English translation, (1952). Science and Method. StateNew York: CityplaceDover.
[5] Andronov A (1929). Les cycles limites de Poincar´e et les th´eorie des oscil- lations auto-entretenues
[6] Li, T.-Y., & Yorke, J.A. (1975). Period 3 implies chaos. American Mathematical Monthly, 82, 985-992.
[7] Henri Poincar´e, L’E´ quilibre d’une masse fluide anim´ee d’un mouvement de rotation, Acta Mathematica, t.7, pp. 259-380, sept 1885.
[8] Lorenz, E.N. (1963). Deterministic non-periodic flow. Journal of Atmo- spheric Science, 20, 130-141.
[9] Lorenz, E.N. (1993). The Essence of Chaos. CitySeattle: PlaceTypeplace- University of PlaceNameWashington Press.
[10] https://cosmolearning.org/courses/nonlinear-dynamics-chaos/video- lectures/
[11] Cartwright, M.I. & Littlewood, J.E. (1945). On nonlinear differential equations of the second order, London Mathematical Society, 20, 180-189.


BachJohann
This is an awesome post. I like this topic.This site has heaps of advantage.I discovered numerous fascinating things from this site. It helps me in numerous ways.Thanks for posting this once more. comprar seguidores instagram boleto
hanafuda earrings
hanafuda earrings
Math Homework Help
Have a maths problem that requires real time instances? Are the maths assignment allotted to you have early deadline? Contact MyAssignmnthelp.com for all types of maths assignment problem. We are the leading math homework help in the U.S., solving all maths problems for the students for last one decade.
BachJohann
A debt of gratitude is in order for setting aside an ideal opportunity to examine this, I feel emphatically about it and love adapting more on this theme. In the event that conceivable, as you pick up aptitude, would you mind upgrading your web journal with additional data? It is greatly useful for me. Stadtwerke Böhmetal
Myassignmenthelp
Get the best myassignmenthelp from the experts of Students Assignment Help at a reasonable price. Our experts provide the reliable assignment help services to the students. Our online expert writers are proficient in writing an assignment.
BachJohann
I have read your article, it is very informative and helpful for me.I admire the valuable information you offer in your articles. Thanks for posting it.. Search Lawyer
Natural Remedies to Boost ‘T’ Levels
The TestRX review at www.TestosteroneOfficial.com offers you detailed information on the ingredients used in the product.
Chaos theory is attentive
Chaos theory is attentive inconsiderate the phase space, or national space of an extensive variety of systems (including actual physical systems). do my homework for me
Read more
Thanks for the nice post. It was very helpful for me. I really like this blog.
ve tranh tuong mam non gia re
Read more !!!
Thanks for the nice post. It was very helpful for me. I really like this blog. Thank you for sharing with us. I find it very helpful for me and allow me to share it.
ve tranh tuong mam non gia re
the rake game download
Thanks for the post.
Nice
you are providing good information
aboutallpet
theory
When a company and or business organization ensures gender balancing in their business, there is increased unity. product description writer
Air china Airlines phone number
Air China is also best at providing services to its passengers and assisting them at every step they need us. If you are facing any problem at any step, call our experts, who are professional and trained. Air China is giving major discounts and amazing offers on airfares. So, connect us at Air China Airlines Phone number to book your tickets now!
southwest airlines phone number
Our expert will help to provide you with the best deals and offers on your tickets. All you have to do is call at our Southwest Airlines Phone Number. When you book your flight with us, you will save money and time because we are offering you the best packages which will not affect much in your budget. So now, just pack your bag without worries and visit your favourite destinations!
American Airlines Phone Number
When someone is going to cancel a flight ticket online or offline, then it generally depends upon the type of tickets purchased. So as per the American airlines‘ official site, you must have a purchase a refundable ticket that helps change and cancel a flight ticket online or you can directly call at American Airlines Phone Number team.
Emirates Airways Official site
Emirates will take care of all your needs regarding your journey. It is set with a massive variety of technical functionalities and utilities that make it a useful place for the best vacation planning. Emirates Airways Official Site has all the value, utility and advantages for its customer.
southwest airlines phone number
Southwest Airlines allows one personal item, one carry-on item and two checked baggage free with your base ticket price. Every additional baggage must be purchased separately. To avoid the hassle, just contact Southwest Airlines Phone Number and they book your extra bags within a few minutes.
All you need to know about
All you need to know about how to start in real sport is here
https://gym-expert.com
Oh, I tried to unterstand
Oh, I tried to unterstand Chaos Theory on my own, but this is too hard. I even asked guys from writing service where I wanted to do my assignment to make this assignmnent and find a solution. But they said this is too hard.
Our team
Our team is motivated and dedicated to providing you a seamless experience when it comes.
buy csgo smurf
dslr camera
hey your blog is useful if you want buy dsl camera you can visit. anyone can save good amount of money you buy best dsrl camera.
I recently watched dark which
I recently watched dark which helped me in building an interest in science. After that, I watched youtube videos related to various scientific theories. And the chaos theory was among them. I am not an expert but have read about it and have a bit of basic knowledge too. And the way you explained this theory was also great. However, it took me some time to understand the things which you talked about. But in the end, I was glad that what you were trying to say. Everything on this webpage was nice except for the loading time of your page. It took your site more than a minute to properly load and was a bit frustrating for me. I think you should look to work on this area can and can own hosting with Bluehost as the Bluehost Black Friday Sale is coming. Overall it was a nice experience reaching your site.
Phase Space is a mathematical
Phase Space is a mathematical representation of the state of a system in two or three dimensions and there is much confusion over who introduced the concept of phase space. - Pest Control Tustin
The scientist does not study
The scientist does not study nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful. If nature were not beautiful, it would not be worth knowing, and if nature were not worth knowing, life would not be worth living”.
spider solitaire
Phase Space is a mathematical
Phase Space is a mathematical representation of the state of a system in two or three dimensions and there is much confusion over who introduced the concept of phase space.
A/C Repair Service
Do you have the guts to play
Do you have the guts to play and prevail in the card game? Although Spider Solitaire 2 suit is relatively similar to Spider Solitaire 1 suit, the game is more challenging to win because it is updated rather than integrated across two decks.
Pretty good post. I just
Pretty good post. I just stumbled upon your blog and wanted to say that I have really enjoyed reading your blog posts. Any way I'll be subscribing to your feed and I hope you post again soon. Big thanks for the useful info. ЕКСТРЕННА ІНДІЙСЬКА ВІЗА
I am constantly surprised by
I am constantly surprised by the amount of information accessible on this subject. What you presented was well researched and well written to get your stand on this over to all your readers. Thanks a lot my dear. Application sa India nga Visa
Thank you very much for this
Thank you very much for this great post. KANADOS MEDICINOS VIZA
Pretty nice post. I just
Pretty nice post. I just stumbled upon your weblog and wanted to say that I have really enjoyed browsing your blog posts. After all I’ll be subscribing to your feed and I hope you write again soon! SOLICITUDE DE VISA E INDIA
This article was written by a
This article was written by a real thinking writer without a doubt. I agree many of the with the solid points made by the writer. I’ll be back day in and day for further new updates. Under 70$ blackpods
Wow, cool post. I’d like to
Wow, cool post. I’d like to write like this too – taking time and real hard work to make a great article… but I put things off too much and never seem to get started. Thanks though. የህንድ ሜዲካል ቪዛ
This is a great article
This is a great article thanks for sharing this informative information. I will visit your blog regularly for some latest post. I will visit your blog regularly for Some latest post. Tyrkiet visumansøgning
mtom
Once I initially commented I clicked the -Notify me when new comments are added- checkbox and now each time a comment is added I get four emails with the same comment. Is there any method you can take away me from that service? Thanks! Buy adderall 30mg
An interesting dialogue is
An interesting dialogue is price comment. I feel that it is best to write more on this matter, it may not be a taboo topic however usually individuals are not enough to talk on such topics. To the next. Cheers. Best SEO experts
This is very educational
This is very educational content and written well for a change. It's nice to see that some people still understand how to write a quality post! Visa India 5 Tahun
Your blog provided us with
Your blog provided us with valuable information to work with. Each & every tips of your post are awesome. Thanks a lot for sharing. Keep blogging.. VISA BISNIS KANADA
Thanks for the nice blog. It
Thanks for the nice blog. It was very useful for me. I'm happy I found this blog. Thank you for sharing with us,I too always learn something new from your post. Indická vízová aplikace
mtrom
reading science fiction books is the stuff that i am always into. science fiction really widens my imagination- bathroom remodel
This is truly a great read
This is truly a great read for me. I have bookmarked it and I am looking forward to reading new articles. Keep up the good work!. INDIJAS VĪZAS PIETEIKUMA VEIDLAPA
FL
I just put the link of your blog on my Facebook Wall. very nice blog indeed.~~`:` digital marketing hong kong
You understand your projects
You understand your projects stand out of the crowd. There is something unique about them. It seems to me all of them are brilliant. วีซ่าสำหรับแคนาดา
You’ve got some interesting
You’ve got some interesting points in this article. I would have never considered any of these if I didn’t come across this. Thanks!. BRITISH COLUMBIA FAKE DRIVING LICENCE
Great write-up, I am a big
Great write-up, I am a big believer in commenting on blogs to inform the blog writers know that they’ve added something worthwhile to the world wide web!.. ভারতীয় ভিসা আবেদন
All the contents you
All the contents you mentioned in post is too good and can be very useful. I will keep it in mind, thanks for sharing the information keep updating, looking forward for more posts.Thanks ពាក្យសុំទិដ្ឋាការឥណ្ឌា
james a lot
You really should be a part of a contest first of the most effective blogs over the internet. I am going to suggest this blog!
Cab near me un godalming
I just want to let you know
I just want to let you know that I just check out your site and I find it very interesting and informative.. VISA new zealand visa
I read that Post and got it
I read that Post and got it fine and informative. ویزای نیوزلند آنلاین
ahmed
very great post.
لعبة من سيربح المليون - لعبة جاتا - لعبة زوما - صب واي سيرفرس - العاب كلاش