Lorenz Oscillator- The Lorenz System

“It may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the future. Prediction becomes impossible”. Edward Lorenz
The meteorologist, Edward Lorenz, in 1961, discovered chaos theory inadvertently whilst modeling atmospheric convection and weather patterns. He published a paper in 1963 where he showed how the model produced chaotic behavior by changing the model from a linear to a nonlinear model. To save time during a simulation run on a very basic desktop computer, he started from the middle of a previous simulation session and to his surprise found the output was completely different from a previous output. By truncating five-digit simulation numbers down to three-digit numbers he discovered one of the principles of chaos theory “Sensitive to Initial Conditions (SIC)”. A small change in initial conditions i.e., reducing the number of places of decimals, produced a bigger change in the system as it evolves. What is often quoted in the literature is Lorenz’s famous quote in a presentation in 1972 to the American Association of Scientific research “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas”, which illustrates how very small change in the initial condition produces much bigger changes later. Edward Lorenz showed that for chaos to exist in autonomous ordinary differential equation systems, three variables and two quadratic non-linear elements must be present. However, since then the number of variables can be reduced to two for non-autonomous chaotic system, and one, for discrete chaotic systems. The Lorenz weather system models clockwise and anticlockwise thermal convective air mass rotations in a closed container and the ordinary differential equations used in this model were originally created by Barry Saltzman (1962). Any n-th order nonlinear differential equation can be written as n separate coupled first-order ODEs. For example, the following coupled equations are a reduced form of the Navier-Stokes equations that model the Lorenz chaotic system that we will examine shortly:
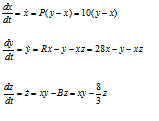
By coupled we mean that the equations are linked to each other and the parameters. The original parameter used by Lorenz are: Prandtl number = 10, Rayleigh number, R = 28, and β = B = 8/3 and are all greater than zero. This simplified Lorenz model has since been proved to be chaotic by B Hassard and J Zhang, 1994 but also by Tucker in 1999. The parameters were given these names because Lorenz derived his equations from the Raleigh-Bénard convection flow (convection in a liquid heated in a container from below, generates Bénard cells). We rewrite these equations in a different form shortly, where we will express the variables as a function of time and introduce initial conditions. The Lorenz equations represent the movement of a horizontal layer of a fluid like air, being heated from below. The speed of the rising air mass, x, is positive for clockwise rotation and negative for anti-clockwise rotations. The temperature difference between descending and ascending air masses is y, and z is the deviation of the temperature profile from a linear scale.
3.1 Simulating the Lorenz system using ABM parts
To simulate the Lorenz system in PSpice, we rearrange the equations in integral form and introduce initial condition conditions x(t0), y(t0), z(t0) for each system variable. We do this because we will implement these equations using integrators using analog behavioral models (ABM) parts which will be replaced by electronic inverting integrators circuits later. The initial conditions will be dropped for simplicity later but will be included in the simulation model as initial conditions on the integrators. Hence, the first equation, P(y-x), becomes –P(x-y). We could use non-inverting integrators but it’s a little more complicated and left as an exercise to the interested reader. Later, we will see how to use the four-quadrant AD633 multiplier IC to realize the nonlinear product terms. This IC may also be configured to achieve integration using current outputs but that’s much later. The Lorenz equations with initial conditions, t0 are:
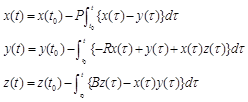
The simplest approach when investigating a chaotic system for the first time is to always use ABM parts, as shown in Figure 1 and later with actual integrated circuit models. This approach is also useful when the circuit becomes complex and in some cases when the electronic part models cause convergence.
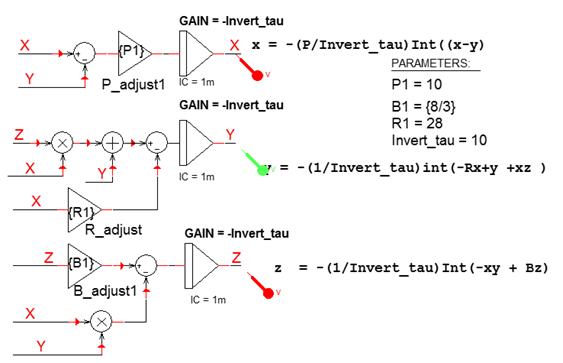
Figure 1: The Lorenz ABM schematic
The ABM INTEG part has its gain set to {–Invert_tau}, where the time constant defined in a PARAM part. The gain of an inverting integrator is set negative and equal to the inverse of the time constant because in the next blog we will use inverting electronic part models. Making the gain as the inverse of the time constant enables us to set a frequency close to the main operating frequency of the system, and in the section on scaling later in this chapter, we will see the need for scaling and how to scale both amplitude and time variables. Figure 2 shows how the three variables vary over time
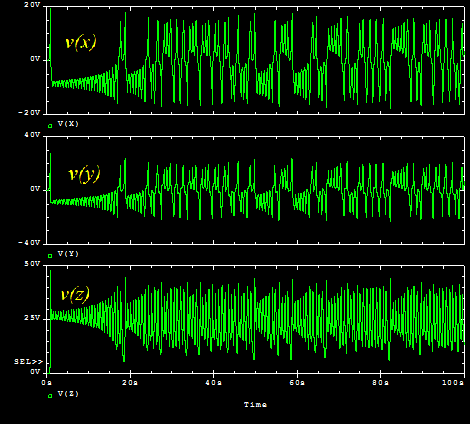
Figure 2: The Lorenz x, y and z output
Figure 3 displays the spectra for the variables and is obtained by pressing the FFT icon when in the Probe environment (appears after simulation). Note we may express the spectral components as dB(V(x)*V(x)), to ensure the smaller spectral component are emphasized, otherwise the main spectral component of 1.32 Hz will tend to mask the other components. Select the Add Trace icon (a small graph-like icon), and then select dB( ) from the list of functions in the right panel. Select between the brackets and type v(x)*v(x). However, I just checked before going to press and the dB() function doesn’t now seem to allow the product of variables in the brackets so instead use 10*log10(v(x)*v(x)). Increasing the simulation run time will increase the frequency resolution but obviously increases the simulation time. The z output is quite periodic and is therefore said to be chaotically weak.
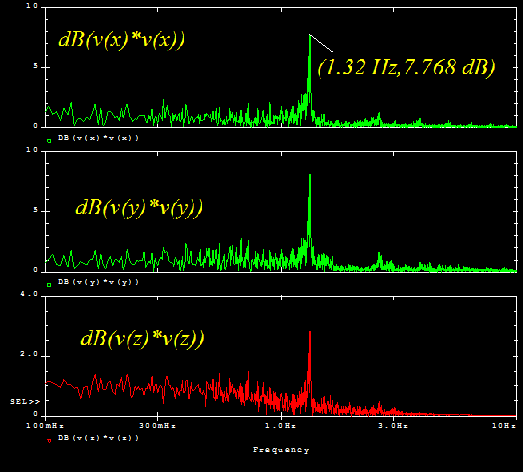
Figure 3: Power Spectra
After Probe simulation and to automate the process of placing multiple windows and additional plots, we use the log command which records all keys selected. Select log in Probe File menu. When this is selected, it will record log file of all keys pressed when doing tasks such as separating the windows. This is useful where you intend to repeat the simulation for parameter variations, for example. If you change the integrator gain from 100 to 1, you will change the system operating frequency hence you will need to change the simulation settings. I have included a log file I created called Lorenz.cmd which will plot all the variables and is called from the File menu in Probe. Select Run Commands and then select Lorenz.cmd. This will plot Figure 1 and 2 but also it will plot the famous Lorenz strange attractor by changing time to the x variable.


This is really helpful post
This is really helpful post and very informative there is no doubt about it. Thanks for sharing such an amazing post with us. resort in alleppey backwater resort alleppey alleppey resort package
Female to male full body to body massage center Delhi
thanks for sharing.
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
<a href="https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...">Female to male Body to Body massage in Delhi</a>
<a href="http://www.bestspaservice.com/">Female to male Body to Body massage in Delhi</a>
<a href="http://www.bestspaservice.com/spa-in-delhi/">Body to Body massage in Delhi</a>
<a href="https://bestspacentreindelhi.blogspot.com/">male to Female Body to Body massage in Delhi</a>
<a href="https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...">Nuru Body to Body massage in Delhi</a>
<a href="https://goo.gl/maps/SukNj6FuoSB2">Full Body to Body massage in Delhi</a>
<a href="http://www.bestspaservice.com/soapy-massage-delhi/">Female to male Body to Body massage center in Delhi</a>
<a href="
http://www.bestspaservice.com/erotic-massage-in-delhi/">Happy Ending Body to Body massage in Delhi</a>
<a href="http://www.bestspaservice.com/body-body-massage/">Body to Body Spa in Delhi</a>
<a href="http://ultimatemassage.in/">Female to male Erotic Body to Body massage in Delhi</a>
<a href="http://www.bodytobodynurumassageindelhi.com/">Female to male Sensual Body to Body massage in Delhi</a>
Body massage center in Delhi | Nuru massage in Delhi | Erotic
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
rekomendasi tas selempang
rekomendasi tas selempang pria jual tas selempang pria murah di Bandung buka tautan ini tas sekolah paling modis dan keren 2020 jual tas ransel pria murah read more read more 5 tas ransel anak paling recommended toko tas murah Bandung tas ransel anak murah tas sekolah anak keren 2020 baca selengkapnya buka tautan ini tas sekolah paling modis dan keren 2020 klik di sini review Right Pack Signature 2nd Edition
hanafuda earrings
hanafuda earrings
Table Tennis Table
Look Very Very impressive plz keep it up. Table Tennis Table Manufacturers gives best wishes for your work.
Gymnastics Equipment
Your work looks very impressive. keep it up Gymnastics Equipment Manufacturers saying thanks for this.
Full body to body massage center in Delhi
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
v
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
Body Spa in Delhi
Amrita Spa is best full body to body massage in delhi - We provide a high level of relaxation massage service in malviya nagar, delhi.
http://www.amritabodyspa.com/
http://www.amritaspa.in/
body massage in delhi
http://femaletomalebodytobodymassageindelhi.wordpress.com/
http://femaletomalebodytobodymassageindelhi.wordpress.com/2017/11/13/female-to-male-body-to-body-massage-in-delhi/
http://delhi.cracker.com/TherapeuticMassage/female-to-male-body-to-body-massage-in-delhi/33285733
http://delhi.cracker.com/TherapeuticMassage/full-body-to-body-massage-in-delhi-by-female-at-amrita-spa/45702877
http://delhi.cracker.com/TherapeuticMassage/female-to-male-body-massage-parlour-in-south-delhi/32902562
https://sites.google.com/site/amritabodyspa/
http://www.body-massage.co.in/amrita-spa-in-malviya-nagar/
http://amritabodyspa.wixsite.com/amritabodyspa
Northern Ireland Health Insurance
Wellness Rewards are a leading supplier of health insurance in Northern Ireland, Belfast. Northern Ireland Health Insurance
Body massage
Female to male full body massage centres in rangpuri, mahipalpur near indira gandhi international airport new delhi at geetanjali spa.
http://www.geetanjalispa.in/
http://delhi.locanto.net/ID_1167718098/Female-to-Male-Full-Body-to-Body-Massage-Center-in-Mahipalpur.html
http://bodymassagemahipalpurigiairportdelhi.wordpress.com/
http://delhi.cracker.com/TherapeuticMassage/female-to-male-body-to-body-massage-in-mahipalpur-delhi/42145748
http://www.body-massage.co.in/female-to-male-body-to-body-massage-near-delhi-airport/
http://sites.google.com/view/body-massage-igi-airport/
http://www.amritabodyspa.com/blog/full-body-massage-near-delhi-airport/
http://www.amritabodyspa.com/blog/female-to-male-body-massage-center-in-mahipalpur/
http://www.body-massage.co.in/full-body-massage-services-in-mahipalpur/
Body massage
High level of relaxation female to male full body to body massage in delhi from head to toe.
http://www.bodytobodymassage.co.in/
http://www.fullbodytobodymassage.com/
https://delhibodytobodymassage.weebly.com/
http://www.oclicker.com/in/Services/Parlours-Salons/Full-Body-to-Body-Massage-in-Delhi-by-Female-to-Male-ad5841
Body to body massage in Delhi
lovely post thanks for share
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
https://delhi.locanto.net/ID_1834590251/Female-To-Male-Body-To-Body-Erot...
https://bestspacentreindelhi.blogspot.com/
https://goo.gl/maps/SukNj6FuoSB2
http://www.bestspaservice.com/
http://www.bestspaservice.com/soapy-massage-delhi/
http://www.bestspaservice.com/body-body-massage/
http://www.bestspaservice.com/erotic-massage-in-delhi/
http://www.bestspaservice.com/spa-in-delhi/
http://ultimatemassage.in/
http://www.bodytobodynurumassageindelhi.com/
https://femaletomalespaindelhi.blogspot.com/2018/04/body-to-body-nuru-ma...
Omega Spa
We are offering all types of body massage to satisfy clients need and provide full relaxation for them. http://www.omegaspa.in/ http://bodytobodymassagelajpatnagardelhi.wordpress.com/ http://www.body-massage.co.in/erotic-massage-in-lajpat-nagar-delhi-by-female-and-male/ http://www.amritabodyspa.com/blog/full-body-to-body-massage-parlor-in-lajpat-nagar-delhi-by-female-to-male/
free look tricks
llo there mates, it is incredible composed piece completely characterized, proceed with the great work always. free look tricks
SEO ΠΩΣ ΚΑΝΩ
llo there mates, it is incredible composed piece completely characterized, proceed with the great work always. SEO ΠΩΣ ΚΑΝΩ
How Many Per Day You Should Do
How Many Per Day You Should Do I'm hoping you keep writing like this. I love how careful and in depth you go on this topic. Keep up the great work.
Interesting
Greatstuff https://german-dating-sites.de/ have used it as well. I also would like to one for my college to increase the interest of mathematics in them. Thanks a lot for sharing http://living-in-switzerland.ch/dating-sites/ keep up the good work guys and thanks again
Body massage
Professional complete full body to body massage parlour in gurgaon & delhi.
http://www.body-massage.co.in/
http://www.body-massage.co.in/24-hours-body-massage-parlours-in-malviya-nagar-delhi/
http://www.body-massage.co.in/b2b-massage-parlour-in-malviya-nagar-delhi/
http://www.body-massage.co.in/body-massage-parlour-in-kashmiri-gate/
http://www.body-massage.co.in/full-body-massage-parlour-in-saket-by-female-to-male/
http://www.body-massage.co.in/body-to-body-massage-parlour-in-mahipalpur/
http://www.body-massage.co.in/female-to-male-body-to-body-massage-price-in-delhi/
http://www.body-massage.co.in/full-body-to-body-massage-in-kalkaji-delhi/
http://www.body-massage.co.in/cross-full-body-massage-parlour-in-delhi-ncr-and-gurgaon/
http://www.body-massage.co.in/full-body-to-body-massage-parlour-aiims-delhi/
http://www.body-massage.co.in/full-body-massage-parlour-in-lajpat-nagar-delhi/
http://www.body-massage.co.in/body-to-body-massage-parlour-in-delhi/
http://www.body-massage.co.in/full-body-massage-parlour-in-sohna-road-gurgaon/
http://www.body-massage.co.in/body-massage-parlour-in-mg-road-gurgaon/
http://www.body-massage.co.in/full-body-to-body-massage-spa-in-mg-road-gurgaon/
http://www.body-massage.co.in/female-to-male-body-massage-in-mg-road-gurgaon/
http://www.body-massage.co.in/full-body-to-body-massage-near-mg-road-metro-station-gurgaon/
http://www.body-massage.co.in/female-to-male-body-to-body-massage-in-mg-road-gurgaon-with-shower/
http://www.body-massage.co.in/body-massage-center-in-gurgaon-near-iffco-chowk/
Erotic massage, nuru massage
Erotic massage, nuru massage and body to body massage in Delhi and NCR is the way to feel you more relax and enjoyment. This is the most popular therapy we are providing at our spa center at great price. Visit to book appointment : https://www.delhibodymassage.co/
Sumit Singh
Li Spa Saket Delhi. The decoration sets the mood for your journey towards physical and spiritual well being.
http://www.lispa.in/
http://www.lispa.in/body-2-body-massage-in-delhi-ncr
http://www.lispa.in/full-body-massage-in-delhi-ncr
http://www.lispa.in/deep-tissue-massage-in-delhi-ncr
http://www.lispa.in/female-to-male-massage-in-delhi-ncr
http://www.lispa.in/happy-ending-massage-in-delhi-ncr
http://fullbodytobodymassageinsaketdelhi.wordpress.com/
http://sites.google.com/view/body-massage-saket-delhi/
http://www.driveat.com/Female-to-Male-Body-to-Body-Massage-in-Saket-Delhi-at-LiSpa-1275591.html
http://www.body-massage.co.in/body-massage-centres-in-select-city-walk-mall-saket/
http://www.oclicker.com/in/Services/Parlours-Salons/Full-Body-Massage-Centres-in-Saket-Delhi-ad5050
http://www.body-massage.co.in/female-to-male-full-body-massage-in-saket-delhi/
Gurgaon Guest House
Enjoy the luxury of staying at house on rent in gurgaon, use HOTEL and get discount on your guest house booking. Gurgaon guesthouse offers cosy, clean rooms with modern facilities and wonderful service.
http://www.gurgaonguesthouse.co.in/
http://www.gurgaonguesthouse.co.in/about/
http://www.gurgaonguesthouse.co.in/directions/
http://www.gurgaonguesthouse.co.in/attractions-gallery/
http://www.gurgaonguesthouse.co.in/faq/
http://www.gurgaonguesthouse.co.in/room-category/room-listings/
http://www.gurgaonguesthouse.co.in/room/standard-rooms/
http://www.gurgaonguesthouse.co.in/room/deluxe-rooms/
http://www.gurgaonguesthouse.co.in/room/super-deluxe-rooms/
http://www.gurgaonguesthouse.co.in/room/business-suits/
http://www.gurgaonguesthouse.co.in/our-offers/
http://www.gurgaonguesthouse.co.in/menu/
http://www.gurgaonguesthouse.co.in/privacy-policy/
http://www.gurgaonguesthouse.co.in/terms-conditions/
http://www.gurgaonguesthouse.co.in/blog/
guest house in varanasi
I needed to leave a little remark to help you and wish you a decent continuation. Wishing you the good luck for all your blogging endeavors. guest house in varanasi
Calligraphy
It is incredibly average to see the best inconspicuous components presented in a basic and seeing way. Calligraphy
Macbook Helper
I will truly value the essayist's decision for picking this astounding article proper to my matter.Here is profound depiction about the article matter which helped me more. Macbook Helper
voyance amour
I think I have never observed such web journals ever that has finish things with all points of interest which I need. So sympathetically refresh this ever for us. voyance amour
Startup Consultancy
This is an excellent post I seen thanks to share it. It is really what I wanted to see hope in future you will continue for sharing such a excellent post. Startup Consultancy
Body massage
Erotic Full Body to Body Massage in Delhi & Gurgaon by Female to Male
http://delhi.locanto.net/ID_1332417206/Pay-Rs-999-Full-Body-Massage-By-Female-to-Male-at-Malviya-Nagar.html
http://delhi.locanto.net/ID_1566893969/Pay-999-Full-Body-Massage-Parlour-in-Saket-Select-City-Walk-Mall.html
http://delhi.locanto.net/ID_213678440/Female-to-Male-Full-Body-to-Body-Massage-Parlour-in-Hauz-Khas.html
http://delhi.locanto.net/ID_912092337/Female-to-Male-Full-Body-to-Body-Massage-in-Lajpat-Nagar.html
http://delhi.locanto.net/ID_278266076/Full-Body-to-Body-Massage-Parlour-in-Delhi-from-Beautiful-Models.html
http://delhi.locanto.net/ID_233528197/Body-to-Body-Full-Nude-Massage-Service-SPA-with-Happy-Ending.html
http://gurgaon.locanto.net/ID_193025517/Female-to-Male-Full-body-Massage-Parlour-in-Gurgaon.html
http://delhi.locanto.net/ID_1332121494/Male-to-Male-Full-Body-Massage-Services-In-Gurgaon-and-Delhi-NCR.html
http://delhi.locanto.net/ID_1167718098/Female-to-Male-Full-Body-to-Body-Massage-Center-in-Mahipalpur.html
sewer repair
I've been searching for information on this theme for some time. I'm cheerful this one is so extraordinary. Keep up the fantastic work. sewer repair
Great info! I recently came
Great info! I recently came across your blog and have been reading along. I thought I would leave my first comment. I don’t know what to say except that I have. Test for Industrial Organizational Psychology 5th Edition by Levy
Tamil News
I would highly appreciate if you guide me through this. Thanks for the article… Nice One... For Tamil News Visit.. https://www.maalaimalar.com/ https://www.dailythanthi.com/
pollution mask
Nobody can live without Prana. We believe that breathing fresh and clean air should be everyone’s basic right. Therefore, our mission is to provide high quality – yet affordable –, anti-pollution solutions, protecting you and your loved ones from the life-threatening effects of polluted air. pollution mask
Online booking system
Its most noticeably awful piece was that the product just worked discontinuously and the information was not exact. You clearly canot go up against anybody about what you have found if the data isn't right. Online booking system
london chauffeur service prices
Unbelievable Blog! I should need to thank for the undertakings you have made in creating this post. I am believing a comparable best work from you later on too. I expected to thank you for this locales! Thankful for sharing. Inconceivable locales! london chauffeur service prices
Wwe Live news, Recap, Result, 2018 Greatest Royal Ruble, Raw
WWE 2018 Raw Roman Reigns vs. Sheamus
WWE Raw 2018 Randy Orton VS Roman Reigns 2018
Full Match- John Cena Vs Edge World Heavy Weight Title Match 2018
Led Lcd Tv Repairing Course in Delhi
Thank you so much for this blog. I am electronics student and this blog helped me alot.
http://www.abcmobileinstitute.com/
http://www.abcmobileinstitute.com/led-lcd-smart-tv-repairing-course.html
http://www.abcmobileinstitute.com/about.html
http://www.abcmobileinstitute.com/computer-hardware-repairing-course.html
http://www.abcmobileinstitute.com/mobile-repairing-course.html
best spa in delhi ncr
Best spa in delhi http://spakailashcolonydelhi.nicedeals.co.in/ http://sparajourigardendelhi.nicedeals.co.in/ http://spamotinagardelhi.nicedeals.co.in/ http://spagreaterkailashdelhi.nicedeals.co.in/ http://spalajpatnagardelhi.nicedeals.co.in/ http://find.nicedeals.co.in/ http://www.nicedeals.co.in/blog/female-male-full-body-body-massage-rajouri-garden-delhi/ http://www.nicedeals.co.in/blog/female-male-full-body-body-massage-parlour-moti-nagar-delhi/ http://www.nicedeals.co.in/blog/female-male-full-body-body-massage-centre-in-lajpat-nagar-delhi/ http://www.nicedeals.co.in/blog/full-body-to-body-massage-in-kailash-colony-delhi-female-male/ http://www.nicedeals.co.in/blog/full-body-body-massage-parlour-in-kailash-colony-delhi/ http://www.nicedeals.co.in/blog/full-body-to-body-massage-parlour-greater-kailash-delhi-female/ http://www.nicedeals.co.in/blog/body-to-body-massage-in-kailash-colony-greater-kailash-2-delhi/ http://www.nicedeals.co.in/blog/female-male-body-body-massage-centres-greater-kailash-delhi/ http://www.nicedeals.co.in/blog/female-male-body-body-massage-moti-nagar-delhi/ http://www.nicedeals.co.in/blog/full-body-to-body-massage-centres-in-lajpat-nagar-delhi/ http://www.nicedeals.co.in/blog/best-deals-discount-coupons-full-body-massage-delhi/ full body to body massage kailash colony delhi full body to body massage rajouri garden delhi full body to body massage moti nagar delhi full body to body massage greater kailash delhi full body to body massage lajpat nagar delhi spa deal in delhi http://spalajpatnagardelhi.nicedeals.co.in/massage-therapy/female-to-male-full-body-to-body-massage-in-lajpat-nagar-delhi/ http://sparajourigardendelhi.nicedeals.co.in/massage-therapy/female-to-male-body-to-body-massage-parlour-in-rajouri-garden-delhi/ http://spamotinagardelhi.nicedeals.co.in/massage-therapy/female-to-male-full-body-to-body-massage-parlour-in-moti-nagar-delhi/ http://spagreaterkailashdelhi.nicedeals.co.in/massage-therapy/female-male-body-to-body-massage-in-greater-kailash-delhi/ http://spakailashcolonydelhi.nicedeals.co.in/massage-therapy/female-male-body-to-body-massage-in-kailash-colony-delhi/
carving wooden furniture
Thanks for writing such a good article in the form of tips for seo of a website. It is not clear how many ways a seo can be possible to viral a Domain or URL like <a href="http://www.birchi.in">carved wooden furniture</a>. People always try direct method but most of time these trick don't works for SEO. Your tips are helpful for the person to make good website optimization for me and my websites or blog. This content is so valuable and surely unique that people are happy and really helpful for them. any pressure from your side, neither in the form of request nor hint or reminder in any ways.
Thanks
mygiftcardsite registration
Step by step instructions for registering, activating and checking all of your gift card balances with mygiftcardsite! mygiftcardsite registration
Celebs Wiki | Biography | Height | Weight | Age | Controversies
Rohitash Gaud Wiki | Biography | Height | Weight | Age | Girlfriend | Wife | Affair | Controversies
Anuranjan Awasthi Wiki | Biography | Height | Weight | Age | Girlfriend | Wife | Affair | Controversies
Tigmanshu Dhulia Wiki | Biography | Height | Weight | Age | Girlfriend | Wife | Affair | Controversies
Mobile Repairing Course in Delhi
Thanks for share this amazing article!!! it’s really helpful.I’m just waiting for your next update to come as I like all your posts. I also recommend your visitors to read here
Mobile Repairing Course in Delhi
Mobile Repairing Institute in Delhi
Mobile Repairing Course in India
Mobile Repairing Institute in India
Mobile Repairing Institute in Laxmi Nagar
Mobile Repairing Course in Laxmi Nagar
Laptop Repairing Course in Delhi
Laptop Repairing Institute in Delhi
LED LCD Repairing Institute in Delhi
LED LCD Repairing Course in Delhi
Wellness Spa
Beauty massage parlour in delhi body massage in delhi Full Body Massage For Male By Female In Delhi Spa In South Delhi Body Massage in Delhi NCR body massage in delhi Best Body Massage Centre in Delhi Body to Body Massage in New Delhi Best Massage Parlours Delhi Body To Body Spa In Delhi Full Body Massage Parlour in Delhi Best Spa in Delhi Female to Male Body to Body Massage in Delhi Massage In Delhi Massage Centre in Delhi Spa In South Delhi Happy Ending Massage in Delhi
Led Lcd Repairing Course In Delhi
Your site is very informative & unique.
http://www.mobilerepairingcoursedelhi.com/mobile-repairing/
http://www.mobilerepairingcoursedelhi.com/led-lcd-tv-repairing/
http://www.mobilerepairingcoursedelhi.com/laptop-repairing/
http://www.mobilerepairingcoursedelhi.com/cctv-repairing/
Led Lcd Repairing Course In Delhi
Very good share.. Nice blog. I usually come here to read.
mobile repairing course in delhi
mobile repairing institute in delhi
mobile repairing institute in laxmi nagar
led lcd smart tv repairing course in delhi
led lcd tv repairing course in delhi
led lcd tv repairing course in laxmi nagar
cctv repairing course in delhi
cctv repairing institute in delhi
laptop repairing course in delhi
laptop repairing institute in delhi
AC repairing course in delhi
Wwe Live news, Recap, Result, 2018 Greatest Royal Ruble, Raw
<a href="http://dai.ly/x6ljfvh">WWE Raw Women's Championship</a>
WWE Raw Tag Team Championship
WWE Cruiserweight Championship
<a href="http://dai.ly/x6ljfvh">WWE women's money in the bank match</a>
<a href="http://dai.ly/x6k0cpc">WWE United States Championship</a>
<a href="http://dai.ly/x6jmvpy">WWE SmackDown Women's Championship</a>
<a href="http://dai.ly/x6j9dup">WWE SmackDown Tag Team Championship</a>
<a href="http://dai.ly/x6j6y04">NXT Championship</a>
<a href="http://dai.ly/x6j0rm1">NXT North American Championship</a>
<a href="http://dai.ly/x6iytlw">NXT Tag Team Championship</a>
<a href="http://dai.ly/x6iu6xd">WWE United Kingdom Championship</a>
<a href="http://dai.ly/x6iqm5w">Mae Young Classic</a>
<a href=" http://dai.ly/x6it69i">wwe Royal Rumble</a>
<a href="http://dai.ly/x6iofiz">wwe Royal Rumble 2018</a>
<a href="http://dai.ly/x6gxhuh">Mixed Match Challenge</a>
<a href="http://dai.ly/x6gswkt">WrestleMania Battle Royal</a>
<a href="http://dai.ly/x6ky46s">WWE Greatest Royal Rumble Championship</a>
<a href="http://dai.ly
<a href="http://dai.ly/x6ljfvh">WWE Raw Women's Championship</a>
WWE Raw Tag Team Championship
WWE Cruiserweight Championship
<a href="http://dai.ly/x6ljfvh">WWE women's money in the bank match</a>
<a href="http://dai.ly/x6k0cpc">WWE United States Championship</a>
<a href="http://dai.ly/x6jmvpy">WWE SmackDown Women's Championship</a>
<a href="http://dai.ly/x6j9dup">WWE SmackDown Tag Team Championship</a>
<a href="http://dai.ly/x6j6y04">NXT Championship</a>
<a href="http://dai.ly/x6j0rm1">NXT North American Championship</a>
<a href="http://dai.ly/x6iytlw">NXT Tag Team Championship</a>
<a href="http://dai.ly/x6iu6xd">WWE United Kingdom Championship</a>
<a href="http://dai.ly/x6iqm5w">Mae Young Classic</a>
<a href=" http://dai.ly/x6it69i">wwe Royal Rumble</a>
<a href="http://dai.ly/x6iofiz">wwe Royal Rumble 2018</a>
<a href="http://dai.ly/x6gxhuh">Mixed Match Challenge</a>
<a href="http://dai.ly/x6gswkt">WrestleMania Battle Royal</a>
<a href="http://dai.ly/x6ky46s">WWE Greatest Royal Rumble Championship</a>
Laser Stretch Marks Removal in Delhi
Your article has very unique and reliable information on new topic so i am really impress with your post. Thanks
Laser Stretch Marks Removal in Delhi
Mobile Repairing Course in Delhi
a very nice blog with always a great content over it. I personally like this blog.
mobile repairing course in preet vihar
mobile repairing institute in preet vihar
mobile repairing course in laxmi nagar
mobile repairing institute in shahdara
mobile repairing course in shahdara
mobile repairing course in daryaganj
mobile repairing institute in daryaganj
mobile repairing course in mayur vihar
mobile repairing institute in mayur vihar
mobile repairing institute in Dayanand Vihar
mobile repairing course in Dayanand Vihar
mobile repairing course in Dilshad Garden
mobile repairing course in Delhi
mobile repairing institute in Delhi
mobile repairing institute in Vinod Nagar
mobile repairing course in Vinod Nagar
mobile repairing institute in Ganesh Nagar
mobile repairing course in Ganesh Nagar
mobile repairing course in Jagatpuri
mobile repairing institute in Jagatpuri
mobile repairing institute in noida
mobile repairing course in noida
mobile repairing course in ghaziabad
mobile repairing institute in ghaziabad
You can check the site with
You can check the site with toys for 2 year old girls on top-mom.com. They have good results and can do the best in this topic
Thanks for posting this info. I just want to let you know that I just check out your site and I find it very interesting and informative. I can't wait to read lots of your posts.
Book Cheap Flight Tickets
https://www.ebooktrip.com