Here you will find out latest app notes.
As the use of battery-operated electronic devices become more widespread, so does the need for simulation models used to analyze the operating characteristics of batteries. The most common batteries in use today are: non-rechargeable Alkaline cells, rechargeable Nickel-Cadmium (NICD) cells, Nickel-Metal-Hydride (NIMH) cells, and sealed Lead-Acid cells. This article presents PSpice behavioral models for simulating the four battery types mentioned above.
Battery Variables
All of the battery types modeled here share some common characteristics and deviations from ideal during discharge.
· Only parameters that vary by 15% or more are considered in these models. Parameters that change less than 15% are not considered because the capacity of cells may vary from +/- 20% to +/- 50% when shelf time, number of recharge cycles, and manufacturing variances are taken into account.
· A reduced state of charge is specified for the start because the capacity of a completely charged cell decays with time. For Alkaline cells, this decay takes years to affect the usable capacity. For NICD and Lead-Acid batteries, the decay is 10% to 30% per month.
Note: The term cell is used to indicate a single energy source. The term battery is used to indicate a power source composed of a single cell or several cells.
· The usable capacity of a cell varies depending on the discharge rate. At very low discharge rates (<) 100 hours, all batteries are very efficient. At very fast discharge rates (< 10 hours), the batteries are not as efficient and the usable capacity is lost.
· For pulsed loads with cycle times greater than 10 seconds, a cell gives more total capacity than under a constant load. The rest portion of the pulsed load allows the battery chemistry to recover some of the lost capacity. But, as the pulsed load cycle time becomes less than 1 second, the cell does not have enough time to recover and usable capacity is not increased. In these cases, the RMS value of the pulsed discharge current should be used in the simulation.
· The affect of cell temperature on cell resistance is not modeled because, for the models, the change in resistance versus temperature falls below the 15% change threshold. The cell temperature changes may be accounted for by adjusting the parameters passed to the various cell subcircuits.
Note: Cell temperature affects both the cell resistance and usable capacity. Low cell temperatures reduce the usable capacity; only a slight decrease is noted at high temperatures.
Cell resistance is a function of the cell’s state of charge. Although there is a negligible effect on Lead-Acid and NICD types, Alkaline cells show a 2:1 to 4:1 increase in cell resistance from full charge to full discharge. Still, cell resistance is fairly flat and constant until 80% discharged, when the resistance increases sharply. The sharp fall in cell voltage during discharge can be looked upon as a large increase in cell resistance.
Cell discharge voltage versus temperature is modeled only for NICD subcircuit because the open circuit cell voltage variation with temperature even for a 0°C to 60°C range is much less than the difference in actual cell discharge voltage for the other types.
Figure 1 shows the results of discharging seven identically rated NICD cells to see how well their capacity track. These are old cells, , used every week for 1 to 2 years, and exhibit a 2:1 spread in measured capacity. Alkaline and Lead-Acid batteries have similar variations even between new cells.
The results indicate that there is little practical value in overly accurate models. Therefore, only those battery characteristics that show a 10 to 15% or greater change during discharge are modeled.
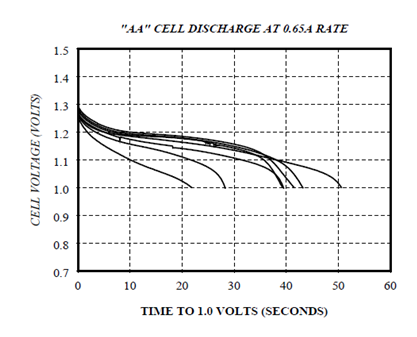
Figure 1: AA Cell Discharge rate
As shown in Figure 2 and Figure 3, the batteries are modeled using the following functional blocks:
To model a cell, perform the following steps:
Link SOC with cell voltage to determine output
Generating a Parameterized PSpice Lookup Table
To model a cell, start by generating a parameterized PSpice lookup table Voltage Controlled Voltage Source (VCVS) using the following steps:
E_Cell +OUT -OUT TABLE {V(x)} = (0,1.5) (0.5,1.3) (1.0,0.0)
Where:
Note: The actual lookup tables are composed of 30 or more pairs of data to provide finer granularity of the resulting discharge voltage curve.
Modeling Discharge Current Sense and Cell Resistance
To model the discharge current sense and the cell resistance, add a zero-valued voltage source in series with the output voltage. The cell resistance is modeled as a simple resistor for NICD or Lead-Acid cells and as a more complex variable resistance that depends on the cell’s state of charge for Alkaline cells.
Modeling the State-of-Charge
To model the state-of-charge (SOC), use a simple and appropriately sized capacitor as the charge storage element that simulates the available charge of the cell. Size this capacitor so that it has a value of 1 Volt at 100% cell capacity and 0.5 Volts at 50% cell capacity. This capacitor is given the following value at the start of the simulation by PSpice’s Parameterization function:
C_CellCapacity 50 0 {3600*CAPACITY*FudgeFactor}
The capacitor, C_CellCapacity, is connected between nodes 50 and 0 and is given a value of the Amp-hour capacity of the cell times a conversion from hours to seconds (3,600 seconds = 1 hour) times a fudge factor (FudgeFactor). If a cell has a 10 Amphour capacity, C_CellCapacity equals10 * 3,600 or 36,000 Farads; this is a big capacitor, but a workable value that is easy to understand.
FudgeFactor adjusts for the difference in the manufacturer’s listed Amp-hour capacity (i.e., some cutoff voltage with some capacity remaining at the cutoff) and the simulated capacity of 0 Volts output at 0% remaining capacity. To correct for this, and still allow the model user to use the manufacturer’s listed capacity, a FudgeFactor value of 1.01 to 1.1 is included.
The actual usable capacity of a cell depends on the rate at which it is being discharged. Most manufacturers list the capacity at the most favorable rate, usually, at greater than 20 hours discharge. At any faster rate, the cell is less efficient and results in a nonlinear function of the discharge rate. This must be characterized as a lookup table at many discharge rates. This inefficiency is modeled as a VCVS in series with the output voltage of the battery state-of-charge node (the voltage on C_CellCapacity). This VCVS subtracts a given amount of capacity from the cell during discharge. The amount subtracted depends on the rate at which the cell is being discharged.
To determine the rate at which the cell is being discharged, it is convenient to normalize the discharge rate in Amps to a more conventional cell rate called the C rate. The C rate is defined as the capacity of the cell in Amp-hours when it is discharged completely in one hour. This normalization makes it easy to determine the cell inefficiency at different rates, and between different cell sizes, because it converts discharge in Amps to discharge in “C” units of the battery capacity at one hour. This conversion is done in the model by the VCVS, E_Rate, as follows.
E_Rate RATE 0 VALUE = {I(V_Sense) / CAPACITY}
E_Rate is the sensed discharge current in Amps divided by the Amp-hour capacity of the cell. The node, RATE, is the instantaneous rate at which the cell is being discharged, as shown in Figure 2.
This instantaneous rate information can almost be fed directly to E_Lost_Rate to determine the actual available capacity. But, when the discharge is a low duty cycle, high value pulsed load, the cell supplies a large initial current which decays in seconds to a lower value. For pulsed loads, the cell recovers between pulses and delivers a higher proportion of its capacity than a cell under constant discharge. The delayed rate is modeled by an RC lowpass filter, as shown Figure 2 as R1 and C1. The exact value of the RC time constant depends on the type and size of cell being simulated. E_Lost_Rate is built like the E_Cell table as follows.
E_Lost_Rate 50 SOC TABLE { V(x) } = (0.0,0.0) (1.5,0.5)
The table entries indicate the capacity unavailable from the cell at high discharge rates. The table entry shows that at a discharge rate of 0, the cell loses 0% of its capacity (first entry). If the discharge rate is 1.5 times the rated capacity of the cell (1.5 C), the cell loses 50% of its capacity (second entry in the table).
In Figure 2, the State-Of-Charge (SOC) node is the subtraction of the voltage on the capacitor C_CellCapacity and E_Lost_Rate. The SOC node represents the capacity in the cell for a given discharge rate during the simulation. G_Discharge discharges C_CellCapacity at the cell rate. The voltage on node 50 relates to the capacity remaining in the cell if the discharge rate is low enough to actually run the cell dry. At low discharge rates, these two nodes are the same; at high discharge rates, node SOC is at a lower potential than node 50. If, at the end of a high discharge rate the cell reverts to a low discharge, nearly the entire rated capacity can be recovered from the cell. At the high discharge rate, approximately 60% of the cell’s rated capacity can be used.
You can now determine the output by linking the state of charge with the cell voltage to determine an output. The state of charge is 1 Volt for 100%, while the cell voltage table is just the opposite. To make the cell voltage correct, the state-of-charge voltage must be inverted as shown in Figure 2. The schematic in Figure 2 represents the subcircuit model common to all batteries without temperature effect.
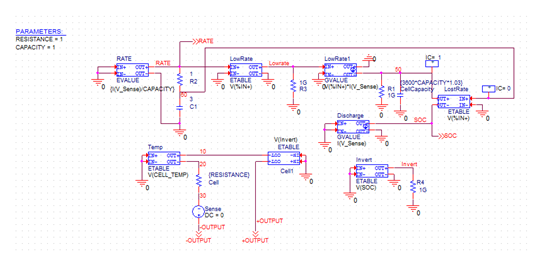
Figure 2: Functional schematic developed for all of teh modeled cell types, only minor changes are required to complete each detailed model type
Alkaline cell resistance is not fixed throughout the discharge.The resistance model is developed by determining the relationship of the output’s current and voltage, then linking this to the battery’s state of charge. The cell has a small resistance increase from 100% to 20% cell capacity, then increases to twice its initial value at 0% capacity.
When the discharge current approaches 100mA, the discharge capacity versus discharge rate produces a kink in the discharge curve. Below 100mA, the cell loses capacity gradually; above 100mA, the rate of lost capacity increases significantly. Although the 100mA discharge rate is the same for all of the cell sizes, the C rating is not. Because it is not possible to relate this kink to a specific C discharge rate, a separate E_Lost_Rate table must be developed for each cell size.
A separate subcircuit model is used to model the 9V Alkaline cell. The cell resistance change versus discharge state is more pronounced in this type of battery, and is modified accordingly in the model.
These cells are often used at very high discharge rates up to 20C. Discharging a fully charged cell in 5 or 6 minutes (10C rate) releases significant amounts of heat. To account for this, a thermal model is included in the cell subcircuit.
The thermal temperature rise of a cell per watt dissipated in free air is approximately Θcell = 13.41 * V-0.61 where V is the cell volume in cubic inches, and Θcell is the thermal rise of the cell in °C per watt dissipated.The thermal time constant for material of the density used in making NICD batteries is approximately 20 minutes per pound or expressed in more convenient terms, 2.65 seconds per gram.
These empirical relationships are used with the calculated cell power dissipation (Cell Discharge Current2 * Cell Resistance) to get a temperature rise and time constant model for the cell temperature. The cell temperature rise above ambient temperature is available at node CELL_TEMP in the NICD model. The temperature information is also used to add or subtract from the cell discharge voltage to account for the cell temperature E_Temp in the NICD model.
Another small modification is made to the NICD model to facilitate the direct entry of manufacturers’ rated capacity data. Most NICD batteries are not rated at their maximum capacity for low discharge rates. The norm is to rate them at the C to C/5 rate, leaving 30% more than the rated capacity if the cell is used at low discharge rates. To account for this difference a Voltage- Controlled Current Source (VCCS), G_LowRate is used to add a small amount of current to C_CellCapacity during discharge at rates less than 1C.
These cells are modeled like the NICD cells, but without the fast discharge thermal effects.
Since these cells are almost universally used in batteries composed of 3, 6, or more cells (6 or 12 Volt batteries), the model is changed slightly. The single cell voltage is multiplied by the number of cells to get the total battery voltage.The schematic in Figure 3 refers to the schematic shown in Figure 2 implemented for NICD battery with an additionally added cell temperature block.

Figure 3: NICD battery discharge models
To use the battery models in a simulation, add the required number of cells to the circuit file, and pass the appropriate parameters to the subcircuit model. The manufacturers’ data sheets may be consulted for information on the cell parameters shown in Table 1.
| Cell Model | Parameter | Meaning |
| ALKALINE | CAPACITY | Capacity of the cell measured at greater than 100 hour discharge time |
| RESISTANCE | Initial cell resistance in ohms | |
| 9V ALKALINE | No parameters are needed for a generic 9 Volt Alkaline battery | |
| NICKELCADMIUM | CAPACITY | Amp-hour capacity of cell measured at the C/5 rate |
| RESISTANCE | Mid-discharge cell resistance in ohms | |
| CELLTEMP1 | Initial cell temperature at start of simulation | |
| VOLUME1 | Volume of cell in cubic inches | |
| WT1 | The weight of the cell in grams | |
| NICKEL METAL HYDRIDE | CAPACITY | Amp-hour capacity of cell measured at the C/5 rate |
| RESISTANCE | Mid-discharge cell resistance in ohms | |
| LEAD-ACID | CAPACITY | Capacity of the battery measured at the 20 hour rate |
| RESISTANCE | Mid-discharge cell resistance in ohms | |
| CELLS | The number of cells that make up the battery(6V = 3 cells, 12V = 6, etc.) |
Note: These parameters are only needed at a discharge rate greater than 5C to account for cell temperature rise.
Since little standardization exists for rating methods between manufacturers, the popular typical parameters are summarized in Table 2 for the most common consumer batteries
| Cell Type | Capacity(Amp-hour) | Resistance(Ohms) | Volume(in3) | Weight(gm) | Cell Number |
| Alkaline Cells | |||||
| Typical subcircuit call for a single Alkaline N cell: | |||||
| X1 +node -node SOC RATE ALKALINE PARAMS: CAPACITY=0.9,RESISTANCE=5 | |||||
| N | 0.0 | 0.8 | - | - | - |
| AAA | 1.2 | 0.6 | - | - | - |
| AA | 2.5 | 0.3 | - | - | - |
| C | 7.5 | 0.2 | - | - | - |
| D | 16.4 | 0.07 | - | - | - |
| Nickel-Cadmium Cells (Standard)1 | |||||
| Typical subcircuit call for a single NICD N cell: | |||||
| X1 +node -node SOC RATE CELL_TEMP NICD PARAMS: CAPACITY=0.15, RESISTANCE=5, VOLUME=0.2, WT=9 | |||||
| N | 0.15 | 0.027 | 0.2 | 9 | - |
| AAA | 0.18 | 0.021 | 0.24 | 10 | - |
| AA | 0.48 | 0.012 | 0.48 | 24 | - |
| SUBC | 1.2 | 0.005 | 1.1 | 50 | - |
| C2 | 1.8 | 0.0045 | 1.6 | 80 | - |
| D2 | 4.0 | 0.0035 | 3.4 | 160 | - |
| Nickel-Cadmium Cells (Standard)1 | |||||
| Typical subcircuit call for a single NICD N cell: | |||||
| X1 +node -node SOC RATE CELL_TEMP NICD PARAMS: CAPACITY=0.15, RESISTANCE=5, VOLUME=0.2, WT=9 | |||||
| AA | 1.1 | 0.03 | - | - | - |
| 4/5A | 1.5 | 0.02(estimated) | - | - | - |
| Lead-Acid Cells | |||||
| Typical subcircuit call for a 6 Volt, 1.3 Amp-hour Lead-Acid battery: | |||||
| X1 +node -node SOC RATE LEADACID PARAMS: CAPACITY=1.3,RESISTANCE=0.06,CELLS=3 | |||||
| 6V-1.3A-hr | 1.3 | 0.06 | - | - | 3 |
| 6V-4.0A-hr | 4.0 | 0.025 | - | - | 3 |
| 6V-6.5A-hr | 6.5 | 0.02 | - | - | 3 |
| 6V-10A-hr | 10 | 0.015 | - | - | 3 |
| 12V-1.3A-hr | 1.3 | 0.12 | - | - | 6 |
| 12V-4.0A-hr | 4.0 | 0.05 | - | - | 6 |
| 12V-6.5A-hr | 6.5 | 0.04 | - | - | 6 |
| 12V-10A-hr | 10 | 0.03 | - | - | 6 |
1. Use the Volume and Weight parameters for NICD cells only to simulate a discharge rate grater than approximately 5C and when the temperature profile of the cell is needed.
2. Although real NICD C and D cells can be purchased, most consumer C and D batteries are actually SUB C cells in a big empty can.
To demonstrate the use of a cell in an actual circuit a real AA NICD cell is discharged into a constant resistance of 2Ohms.
Then the circuit shown in Figure 4 is used with PSpice to simulate the 2Ohm and 5Ohm discharge. Running this circuit with the capacity of the NICD model normalized to the actual capacity of the measured cell, shows results which compare very favorably with the real behavior.
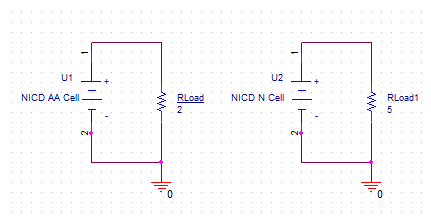
Figure 4: Schematic for NICD AA and N cell Discharge test
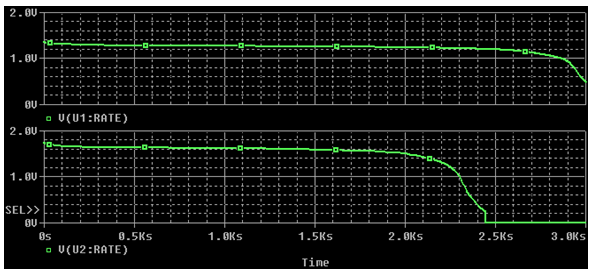
Figure 5: Simulation result of NICD AA and N cell Discharge
N cell is simulated by changing the properties of the cell. The .IC statement sets the initial conditions, and must be set for every subcircuit used. V(X1.50) sets the initial charge on node 50 of the X1 subcircuit. This is the voltage on the battery Amp-hour capacity model which simulates the initial state of charge. Setting this node to 1 Volt equals an initial state of charge of 100%. Likewise, 0.8 Volts would represent an 80% initial state of charge.
The next initial condition ( V(X1.60)=0) sets the voltage on the delayed lost rate calculator to zero. This allows the voltage on capacitor C1 (internal to the subcircuit) to start at 0 Volts as it would if the discharge current was zero before the simulation started. Another way to achieve this result is to switch on the discharge currents just after the simulation starts. This automatically sets the delayed lost rate voltage to zero at the start of the simulation.
Note:To perform simulation of other cell models use the .olb file.
During a fast discharge, the cell temperature of a NICD can change by 25°C or more. The effect of cell temperature on voltage is accounted for in the NICD model by changing the cell voltage based on the calculated temperature. The other models do not incorporate temperature effects directly into the simulation.
The major temperature influence on the cell is capacity. This may be accounted for by adjusting this parameter at the start of a simulation. The following equations give the new capacity for each cell type at any discharge temperature from 0 to 60°C based on the initial capacity at 25°C.
1.Alkaline Cells:
NewCapacity = OldCapacity * (0.85 + 8.64E-3 * T - 1.05E-4 * T*T)
2.Nickel-Cadmium Cells:
If T > 25°C NewCapacity=OldCapacity
If T < 25°C NewCapacity=OldCapacity*(0.815+7.5E-3*T)
3.Nickel-Metal-Hydride Cells:
NewCapacity=OldCapacity*(0.913+1.1E-2*T-3.0E-4*T*T)
4.Lead-Acid Cells:
NewCapacity=OldCapacity*(0.84 + 7.96E-3*T-6.07E-5*T*T)
To use the equations, simply plug in the 25°C initial capacity for OldCapacity and the new discharge temperature for T into the proper equation. If needed, these equations can also be built into the subcircuit models.
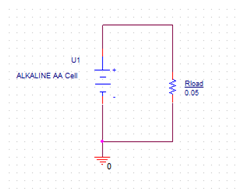
Figure 6: Schematic for Alkaline AA Cell Discharge test
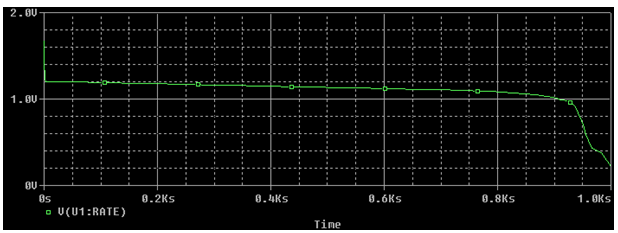
Figure 7: Simulation result of Alkaline AA Cell
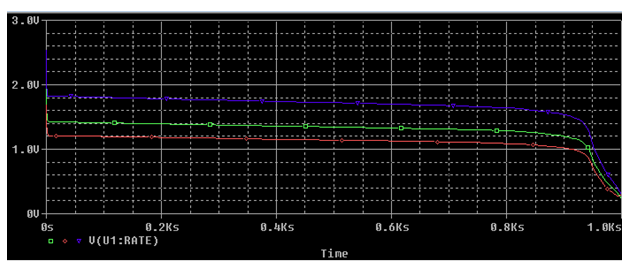
Figure 8: Simulation result of Alkaline AA Cell at different temperatures
Figure 8 shows the simulation results for the discharging rate of Alkaline AA cell at 0, 25, and 100°C temperatures corresponding to the green,red and blue color traces respectively.
The circuits presented in this chapter trade off accuracy with simplicity and simulation time. There are several cases where the simulated and actual results vary significantly.
Usage beyond standard cutoff voltages not accounted for: The models were designed to be used with the standard cutoff voltages as specified by the battery makers. For NICD batteries, this is 0.8 to 1.1 Volts per cell. For Alkaline cells, the cutoff is 0.8 to 1.2 Volts per cell. For Lead-Acid cells, the cutoff voltage is typically 1.5 to 1.7 Volts per cell. Usage beyond these limits should be studied carefully because they are not specifically accounted for in the modeling process.
Models not designed for parallel connection: These models are not designed to be connected in parallel.This is not acceptable in consumer design anyway, because there is no way to guard against the end user putting an Alkaline cell in parallel with a NICD or Carbon cell. If these different types of cells are connected together, the charge most likely will not equalize. This results in overcharging and leakage of the weak cell, causing damage.
The goal of simulation is to obtain results faster than can be achieved with the hardware, or to measure behaviors which cannot easily be accessed in the hardware. The following notes should help when making speed/accuracy trade-offs.
The following are the five different Cell discharge models.These models are presented in the library file battery.lib and its associated symbols are presented in the battery.olb file.These .lib and .olb files can be used to perform discharge test of other batteries.
** PSpice Alkaline battery discharge model **
.SUBCKT ALKALINE +OUTPUT -OUTPUT SOC RATE + PARAMS: CAPACITY=1, RESISTANCE=1
C_CellCapacity 50 0 { 3600 * CAPACITY * 1.01 }
R1 50 0 1G
E_Resistance 20 10 VALUE = {I(V_Sense) * RESISTANCE * V(Cell_Res)}
E_Cell_R Cell_Res 0 TABLE { V(50) } = (0,2) (0.2,1) (1,1)
R3 Cell_Res 0 1G
V_Sense -OUTPUT 20 0
E_Invert Invert 0 TABLE { V(SOC) } = (0,1) (1,0)
R4 Invert 0 1G
E_Rate RATE 0 VALUE = { I(V_Sense)/CAPACITY }
R2 RATE 60 10
C1 60 0 1
G_Discharge SOC 0 VALUE = { I(V_Sense) }
E_Lost_Rate 50 SOC TABLE { V(60) } =
* * Use one of the following tables!!! * *
;----- Use this table for N cells -----
;+ (0.0,0.0) (0.019,0.056) (0.043,0.13) (0.072,0.28)
;+ (0.12,0.39) (0.21,0.58) (0.31,0.69)
;----- Use this table for AAA and AA cells -----
;+ (0.0,0.0) (0.018,0.08) (0.043,0.14) (0.08,0.2)
;+ (0.14,0.3) (0.26,0.48) (0.4,0.6)
;----- Use this table for C cells -----
;+ (0.0,0.0) (0.17,0.13) (0.035,0.31) (0.055,0.45)
;+ (0.093,0.53) (0.17,0.65) (0.27,0.73)
;----- Use this table for D cells -----
;+ (0.0,0.0) (0.0091,0.091) (0.017,0.15) (0.032,0.36)
;+ (0.058,0.42) (0.079,0.61) (0.13,0.73) (0.18,0.82)
E_Cell +OUTPUT 10 TABLE { V(Invert) }=
+ (0.000E+00 1.528E+00) (2.320E-03 1.511E+00) (4.640E-03 1.500E+00)
+ (9.280E-03 1.481E+00) (1.392E-02 1.468E+00) (1.856E-02 1.457E+00)
+ (2.552E-02 1.442E+00) (3.248E-02 1.430E+00) (3.944E-02 1.419E+00)
+ (4.872E-02 1.406E+00) (5.800E-02 1.394E+00) (6.728E-02 1.380E+00)
+ (7.656E-02 1.370E+00) (1.206E-01 1.326E+00) (2.691E-01 1.230E+00)
+ (5.522E-01 1.126E+00) (8.213E-01 1.021E+00) (9.025E-01 9.901E-01)
+ (9.257E-01 9.792E-01) (9.443E-01 9.676E-01) (9.559E-01 9.564E-01)
+ (9.628E-01 9.445E-01) (9.698E-01 9.299E-01) (9.744E-01 9.181E-01)
+ (9.791E-01 9.043E-01) (9.814E-01 8.937E-01) (9.837E-01 8.800E-01)
+ (9.860E-01 8.654E-01) (9.884E-01 8.470E-01) (9.907E-01 8.040E-01)
+ (9.930E-01 6.417E-01) (9.953E-01 3.795E-01) (9.976E-01 3.354E-01)
+ (1.0 0.0)
.ENDS
** PSpice 9 Volt Alkaline battery discharge model **
.SUBCKT ALK_9V +OUTPUT -OUTPUT SOC RATE + PARAMS: CAPACITY=0.565
E_Rate RATE 0 VALUE = { I(V_Sense)/CAPACITY }
R2 RATE 60 10
C1 60 0 1
G_Discharge SOC 0 VALUE = { I(V_Sense) }
E_Lost_Rate 50 SOC TABLE { V(60) } = + (0.0,0.0) (0.025,0.009) (0.046,0.080) (0.088,0.14) (0.18,0.21) (0.71,0.45)
C_CellCapacity 50 0 { 3600 * CAPACITY * 1.06 }
R1 50 0 1G
E_Resistance 20 10 VALUE = { I(V_Sense) * 2.0 * V(Cell_Res) }
E_Cell_R Cell_Res 0 TABLE { V(50) } = (0,4) (0.2,2) (1,1)
R3 Cell_Res 0 1G
V_Sense -OUTPUT 20 0
E_Invert Invert 0 TABLE { V(SOC) } = (0,1) (1,0)
R4 Invert 0 1G
E_Cell +OUTPUT 10 TABLE { V(Invert) } =
+ (0.00 9.18) (0.05 8.82) (0.10 8.62)
+ (0.15 8.41) (0.20 8.30) (0.25 8.21)
+ (0.30 8.09) (0.35 7.99) (0.40 7.95)
+ (0.45 7.89) (0.50 7.79) (0.55 7.66)
+ (0.60 7.55) (0.70 7.18) (0.75 6.96)
+ (0.80 6.58) (0.85 6.12) (0.90 5.42)
+ (0.95 4.51) (1.00 0.00)
.ENDS
** PSpice Nickel-Cadmium battery discharge model **
.SUBCKT NICD +OUTPUT -OUTPUT SOC RATE CELL_TEMP + PARAMS: CAPACITY=1, RESISTANCE=1, CELLTEMP=25, VOLUME=1, WT=1
E_Rate RATE 0 VALUE = { I(V_Sense)/CAPACITY }
R2 RATE 60 1
C1 60 0 3
E_LowRate LowRate 0 TABLE {V(RATE)} = (0,0) (0.001,0.2) (0.1,0.2) (1,0)
R3 LowRate 0 1G
G_LowRate 0 50 VALUE = { V(LowRate)*I(V_Sense) }
G_Discharge SOC 0 VALUE = { I(V_Sense) }
E_LostRate 50 SOC TABLE { V(60) } = (1.0,0) (10,0.25)
C_CellCapacity 50 0 { 3600 * CAPACITY * 1.03 }
R1 50 0 1G
E_Temp_Rise 70 0 VALUE = {PWR(I(V_Sense),2)*RESISTANCE*(13.4 PWR(VOLUME,-0.6065))}
V_Ambient 80 70 { CELLTEMP }
R_Thermal CELL_TEMP 80 { 2.65 * WT }
C2 CELL_TEMP 0 1
R_Cell 20 30 { RESISTANCE }
E_Temp 10 20 TABLE { V(CELL_TEMP) } = (0,-0.025) (25,0) (60,-0.100)
V_Sense -OUTPUT 30 0
E_Invert Invert 0 TABLE { V(SOC) } = (0,1) (1,0)
R4 Invert 0 1G
E_Cell +OUTPUT 10 TABLE { V(Invert) } =
+ (0.0000000000E+00 1.3148600000E+00) (1.7391197842E-03 1.3114600000E+00)
+ (8.6956352158E-03 1.3008400000E+00) (1.7391252284E-02 1.2910200000E+00)
+ (3.1304265000E-02 1.2794000000E+00) (4.8695517284E-02 1.2685600000E+00)
+ (6.4347649784E-02 1.2608600000E+00) (9.2173675215E-02 1.2504800000E+00)
+ (1.3739093478E-01 1.2401000000E+00) (2.9217314000E-01 1.2300000000E+00)
+ (4.9738998228E-01 1.2199000000E+00) (6.0347665207E-01 1.2099000000E+00)
+ (7.3738938358E-01 1.1909200000E+00) (7.8782396620E-01 1.1801600000E+00)
+ (8.2086740543E-01 1.1705000000E+00) (8.4695429293E-01 1.1602800000E+00)
+ (8.6608462870E-01 1.1501000000E+00) (8.7999764142E-01 1.1403000000E+00)
+ (8.9043241457E-01 1.1309800000E+00) (8.9912806793E-01 1.1212400000E+00)
+ (9.0782372129E-01 1.1090600000E+00) (9.1304106250E-01 1.1001000000E+00)
+ (9.1825840370E-01 1.0899000000E+00) (9.2347583564E-01 1.0784600000E+00)
+ (9.2695405706E-01 1.0705000000E+00) (9.3217141642E-01 1.0586000000E+00)
+ (9.3564971043E-01 1.0508000000E+00) (9.3912795000E-01 1.0430000000E+00)
+ (9.4434529120E-01 1.0303200000E+00) (9.4782360336E-01 1.0207400000E+00)
+ (9.5130184293E-01 1.0102600000E+00) (9.5304094457E-01 1.0046200000E+00)
+ (9.5478006435E-01 9.9866000000E-01) (9.5651918413E-01 9.9248000000E-01)
+ (9.5825830392E-01 9.8596000000E-01) (9.5999749629E-01 9.7910000000E-01)
+ (9.6173659793E-01 9.7178000000E-01) (9.6347571771E-01 9.6386000000E-01)
+ (9.6521483750E-01 9.5520000000E-01) (9.6695395728E-01 9.4556000000E-01)
+ (9.6869307707E-01 9.3460000000E-01) (9.7043217870E-01 9.2192000000E-01)
+ (9.7217137108E-01 9.0686000000E-01) (9.7391049086E-01 8.8908000000E-01)
+ (9.7564961064E-01 8.6722000000E-01) (9.7738873043E-01 8.3990000000E-01)
+ (9.7912783206E-01 8.0636000000E-01) (9.8086695185E-01 7.6520000000E-01)
+ (9.8260607163E-01 7.1436000000E-01) (9.8434519142E-01 6.6000000000E-01)
+ (9.8608438379E-01 6.0778000000E-01) (9.8782348543E-01 5.5698000000E-01)
+ (9.8956260521E-01 5.0776000000E-01) (9.9130172500E-01 4.5810000000E-01)
+ (9.9304084478E-01 4.0860000000E-01) (9.9477996457E-01 3.5850000000E-01)
+ (9.9651906620E-01 3.0526000000E-01) (9.9825825858E-01 2.4604600000E-01)
+ (9.9999737836E-01 1.8616600000E-01) (1.0000000000E+00 0.0000000000E+00)
.ENDS
* PSpice Lead-Acid battery discharge model **
.SUBCKT LEADACID +OUTPUT -OUTPUT SOC RATE + PARAMS: CAPACITY=1, RESISTANCE=1, CELLS=3
E_Rate RATE 0 VALUE = { I(V_Sense)/CAPACITY }
R2 RATE 60 60
C1 60 0 1
G_Discharge SOC 0 VALUE = { I(V_Sense) }
E_Lost_Rate 50 SOC TABLE { V(60) } = + (0.05,0.0) (0.089,0.11)(0.16,0.20)(0.62,0.39)(0.8,0.47) (1.6,0.44)
C_CellCapacity 50 0 { 3600 * CAPACITY * 1.15 }
R1 50 0 1G
R_Cell 10 20 { RESISTANCE }
E_Battery +OUTPUT 10 VALUE = { V(Cell_V) * CELLS }
V_Sense -OUTPUT 20 0
E_Invert Invert 0 TABLE { V(SOC) } = (0,1) (1,0)
R4 Invert 0 1G
R5 Cell_V 0 1G
E_Cell Cell_V 0 TABLE { V(Invert) } =
+ (0.000E+00 2.171E+00) (5.222E-04 2.149E+00) (1.828E-03 2.128E+00)
+ (1.263E-01 2.101E+00) (4.908E-01 2.001E+00) (6.385E-01 1.949E+00)
+ (7.459E-01 1.900E+00) (7.834E-01 1.875E+00) (8.117E-01 1.850E+00)
+ (8.313E-01 1.826E+00) (8.436E-01 1.801E+00) (8.517E-01 1.773E+00)
+ (8.556E-01 1.750E+00) (8.591E-01 1.724E+00) (8.616E-01 1.702E+00)
+ (8.646E-01 1.676E+00) (8.677E-01 1.648E+00) (8.707E-01 1.623E+00)
+ (8.732E-01 1.600E+00) (8.850E-01 1.499E+00) (8.965E-01 1.401E+00)
+ (9.000E-01 1.333E+00) (1.000E+00 0.000E+00)
.ENDS
** PSpice Nickel-Metal-Hydride battery discharge model **
.SUBCKT NIMH +OUTPUT -OUTPUT SOC RATE + PARAMS: CAPACITY=1, RESISTANCE=1
E_Rate RATE 0 VALUE = { I(V_Sense)/CAPACITY }
R2 RATE 60 1
C1 60 0 3
E_LowRate LowRate 0 TABLE {V(RATE)} = (0,0) (0.001,0.15) (0.1,0.1) (0.2,0)
R3 LowRate 0 1G
G_LowRate 0 50 VALUE = { V(LowRate)*I(V_Sense) }
G_Discharge SOC 0 VALUE = { I(V_Sense) }
E_LostRate 50 SOC TABLE { V(60) } = (0.2,0.0) (1.0,0.15) (5,0.2)
C_CellCapacity 50 0 { 3600 * CAPACITY * 1.01 }
R1 50 0 1G
R_Cell 20 30 { RESISTANCE }
V_Sense -OUTPUT 30 0
E_Invert Invert 0 TABLE { V(SOC) } = (0,1) (1,0)
R4 Invert 0 1G
E_Cell +OUTPUT 20 TABLE { V(Invert) } =
+(0.0000E+00 1.3346E+00) (7.0989E-03 1.3244E+00) (1.6327E-02 1.3144E+00)
+(2.9283E-02 1.3042E+00) (4.2593E-02 1.2942E+00) (6.8859E-02 1.2841E+00)
+(1.3008E-01 1.2733E+00) (4.3605E-01 1.2633E+00) (5.1165E-01 1.2532E+00)
+(5.8033E-01 1.2432E+00) (6.4635E-01 1.2331E+00) (7.0190E-01 1.2231E+00)
+(7.5834E-01 1.2130E+00) (8.0324E-01 1.2030E+00) (8.3075E-01 1.1929E+00)
+(8.5116E-01 1.1828E+00) (8.6820E-01 1.1727E+00) (8.8310E-01 1.1627E+00)
+(8.9641E-01 1.1527E+00) (9.0848E-01 1.1425E+00) (9.1860E-01 1.1324E+00)
+(9.2730E-01 1.1223E+00) (9.3475E-01 1.1122E+00) (9.4167E-01 1.1021E+00)
+(9.4841E-01 1.0919E+00) (9.5480E-01 1.0817E+00) (9.6013E-01 1.0716E+00)
+(9.6439E-01 1.0615E+00) (9.6776E-01 1.0515E+00) (9.7060E-01 1.0407E+00)
+(9.7291E-01 1.0299E+00) (9.7486E-01 1.0190E+00) (9.7663E-01 1.0080E+00)
+(9.7823E-01 9.9782E-01) (9.8001E-01 9.8706E-01) (9.8196E-01 9.7630E-01)
+(9.8391E-01 9.6612E-01) (9.8586E-01 9.5606E-01) (9.8799E-01 9.4542E-01)
+(9.9012E-01 9.3524E-01) (9.9225E-01 9.2518E-01) (9.9420E-01 9.1498E-01)
+(9.9580E-01 9.0400E-01) (9.9687E-01 8.9186E-01) (9.9740E-01 8.7990E-01)
+(9.9775E-01 8.6280E-01) (9.9793E-01 8.4818E-01) (9.9811E-01 8.2718E-01)
+(9.9828E-01 7.9518E-01) (9.9846E-01 7.4066E-01) (9.9864E-01 6.4712E-01)
+(9.9882E-01 5.1380E-01) (9.9899E-01 3.3476E-01) (1.0000E+00 0.0000E+00)
.ENDS
1 Hageman, S.C. “PC-based power supply tester slashes setup time to minutes,” Personal Engineering & Instrumentation News, December 1990, Pages 65-66.
2. MicroSim, Circuit Analysis Reference Manual, Version 5.3,1993, MicroSim Corporation, Irvine, CA.
3. DURACELL, Alkaline Dioxide Batteries, DURACELL INC., Bethel, CT.
4. SANYO, Various literature on Nickel-Cadmium batteries,Sanyo Electric Inc., Little Ferry, NJ.
5. Panasonic, Sealed Lead-Acid Batteries - Technical Handbook, Panasonic Industrial Co. Secaucus, NJ.
6. Panasonic, Batteries, Panasonic Industrial Co. Secaucus,NJ.
7. GATES, Rechargeable Batteries - Applications Handbook,1992, ISBN 0-7506-9228-6, Butterworth-Heinemann,Stoneham, MA
8. General Electric, Nickel-Cadmium Battery Application Engineering Handbook, 1975, General Electric Company.
9. Power-Sonic, Battery Selector Guide, Power-Sonic Corp.,Redwood City, CA.
© Copyright 2016 Cadence Design Systems, Inc. All rights reserved. Cadence, the Cadence logo, and Spectre are registered trademarks of Cadence Design Systems, Inc. All others are properties of their respective holders.
Copyright © 2020 Cadence Design Systems, Inc. All rights reserved.
