Modelling Quartz Crystals

This document explains how a Quartz Crystal can be modeled using a series RLC circuit and a parallel (package) Capacitor. Please note that Crystal Oscillators are available in the XTAL.OLB Library under the SPB/OrCAD Installation. 

Equivalent Electrical Model

Crystal oscillators can be modeled as a series RLC circuit along with a parallel capacitor as shown in Figure 1. Quartz crystal oscillators tend to operate towards their “series resonance”.

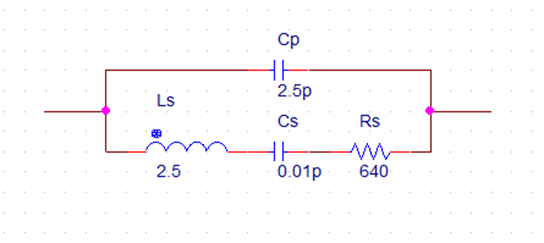
                                       Figure 1: Equivalent Electrical Model

The equivalent impedance of the crystal has a series resonance where Cs resonates with inductance, Ls at the crystals operating frequency. This frequency is called the crystals series frequency, ƒs. As well as this series frequency, there is a second frequency point established as a result of the parallel resonance created when Ls and Cs resonates with the parallel capacitor Cp as described below:

Crystal Impedance against Frequency

R = R and X_LS = 2πfL_s

X_CS=1/2πfC_s and X_CP = 1/2πfC_p

Crystal Reactance against Frequency

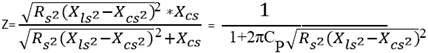
X_S = R²+(X_LS-X_CS)²

X_CP = 1/(2πfC_p ) and X_P = (X_s*X_CP)/(X_s+X_CP )

Series Resonant Frequency

f_s = 1/(2π√ L_s C_s )

Parallel Resonant Frequency

f_p = 1/2π√ L_s (C_p *C_s)/(C_p+C_s ) 

Crystal Oscillators Q-factor

Q = X_L/R = 2πfL/R

If this Q-factor value is high, it contributes to a greater frequency stability of the crystal at its operating frequency making it ideal to construct crystal oscillator circuits.

A Crystal has an extremely high Q-Factor (Quality Factor) of 5000 or more, which leads to very long simulation time for any oscillation to build up.

It is possible that due to numerical range initial amplitude build up may not get propagated to next simulation cycle and the oscillation build up is not visible.

A pulse is injected in the Crystal circuit or Initial Condition specified on Capacitors to accelerate the amplitude build up and speed up simulation.

Simulation results

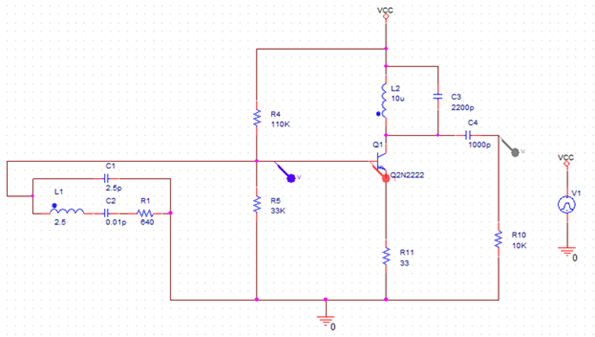
                                                       Figure 2: Circuit diagram

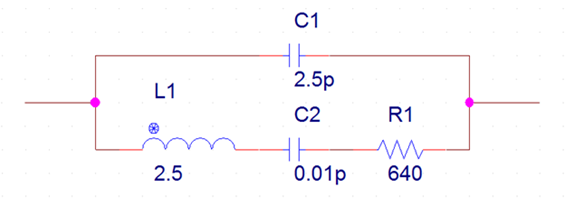
                                   Figure 3: Equivalent Circuit (Model)  Parameters

L1 = 2.5, C2 = 0.01pF, R1 = 640Ω, C1 = 2.5pF

Series Resonant Frequency

f_s = 1/2π√ L_s C_s  = 1/2π√ 2.5*0.01p  = 1.0065MHz

Parallel Resonant Frequency

f_p = 1/2π√ L_s (C_p *C_s)/(C_p+C_s )  = 1/2π√ 2.5(2.5p*0.01p)/(2.5p+0.01p)  = 1.0085MHz

Crystal Oscillators Q-factor

Q = X_L/R = 2πfL/R = (2π*10⁶*2.5)/640 = 0.0245436*10⁶ = 24543 ≈ 25000

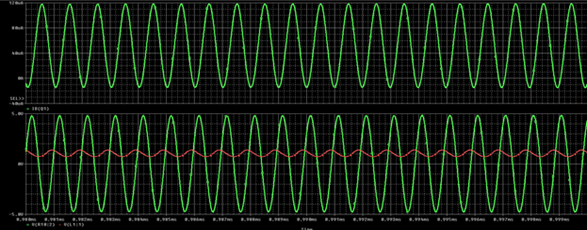
                                                   Figure 4: Simulation Results

© Copyright 2016 Cadence Design Systems, Inc. All rights reserved. Cadence, the Cadence logo, and Spectre are registered trademarks of Cadence Design Systems, Inc. All others are properties of their respective holders